
扇形面积公式 搜狗搜索
R是扇形半径,n是弧所对圆心角度数,π是圆周率,也可以用扇形所在圆的面积除以360再乘以扇形圆心角的角度n S=nπR^2/360 S=1/2LR (L为弧长,R为半径) S=1/2αr平方 拓展资料: 扇形周长公式 因为扇形周长=半径×2弧长 若半径为r,直径为d,扇形所对的圆心角的度数为n°,那么扇形周长: C=2r(n÷36013/2/21 \\\\ 中心角2\pi\,ラジアン(360\Deg)に対する面積は\,\pi r^2\ (円の面積)である \\2zh よって \bm{(中心角)(面積)=\thetaS=2\pi\pi r^2}\ より S=\bunsuu12r^2\theta \\\\ 中学で学習した度数法の場合の以下の公式と比較すると,\ 弧度法がいかに本質的であるかがわかる \bm{扇形とトップ 100 おうぎ形 面積 求め方 円と
扇形 中心 角 公式
扇形 中心 角 公式-15/7/13 扇形の中心角の大きさの求め方を教えてください 当てはめのところで、『360分の中心角 = 分の面積』となっているのですが、 の場所に何が入るかわかる方はいませんか? ここがわからな くて困ってます わかる方教えてください お願いします18/3/15 「扇形の中心角の求め方」の公式 ってチョー便利。 教科書にはのっていない「知る人ぞ知る公式」なんだ。 扇形の中心角をx°、弧の長さをL、半径をrとすると、 x = 180L/πr になるってや
1
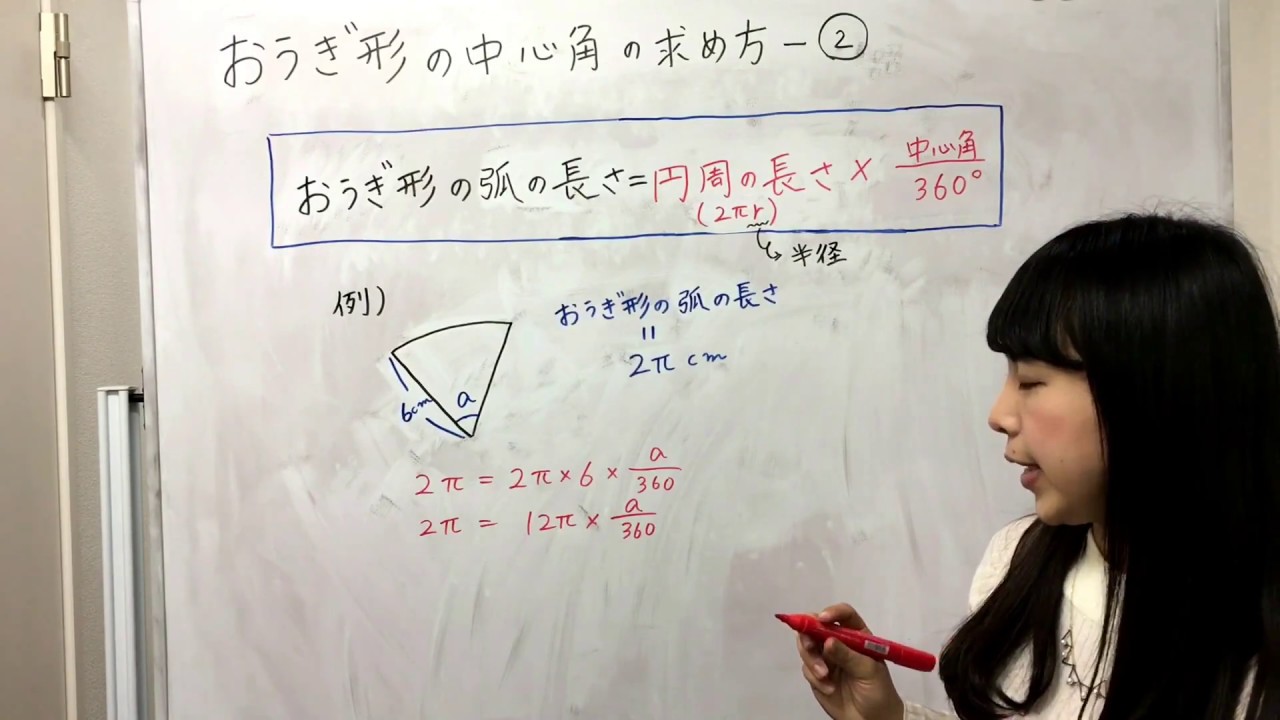
17/3/15 Ken 2分でわかる! 扇形(おうぎ形)の弧の長さの求め方 扇形の「弧の長さの求め方」がよくわからない! ? ? こんにちは、この記事をかいてるKenだよー! パンケーキはハチミツで食べるのがうまいね。2/9/ これを展開した時にできる、側面のおうぎ形の中心角は何度になるでしょうか? まずは一般的な方法で解いてみましょう。 底面の半径が3cmなので、円周=直径×\(π\)=6\(π\) cm となります。18/7/ 圆心角弧度数公式为:L=n× π× r/180,L=α× r。 其中n是圆心角度数(角度制),r是半径,L是圆心角弧长,α是圆心角度数(弧度制), π是圆周率。 在半径是R的圆中,因为360°的圆心角所对的弧长就等于圆周长C=2πr,所以n°圆心角所对的弧长为l=n°πr÷180°(l=n°x2πr/360°)
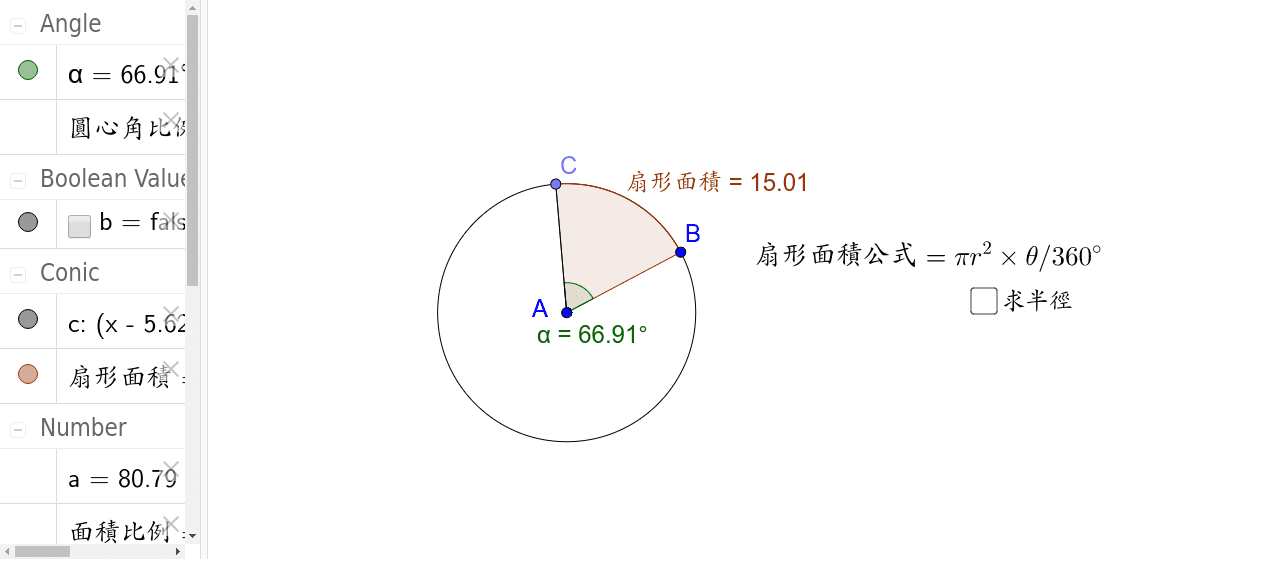
扇形面积S=圆心角的角度(角度制) × 圆周率π314 × 半径r² / 360°Scipursuit 算数・数学 扇形の弧の長さの求め方 公式と計算例 扇形の弧の長さを求める公式は、次の通りです。 l = 2πr× x 360 l = 2 π r × x 360 中心角 x°、半径 r の扇形 ここで、l は扇形の弧の長さ、π は円周率、r は円の半径、x は中心角(単位「度」)を表します。 このページの続きでは、この 公式の導き方 と、 扇形の弧の長さを求める計算問題の解き方 を説明 弧长的计算公式 弧长公式n 是圆心角度数,r 是半径,a 是圆心角弧度。公式 l = n(圆心角)x π(圆周率)x r(半径)/180 在半径是 R 的圆中,因为 360°的圆心角所对的弧长就等于圆周长 C=2πR,所以 n°圆心角所对的弧长为 l=n°πR÷180°。
扇形 中心 角 公式のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  | |
 | ||
「扇形 中心 角 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 | ||
「扇形 中心 角 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 | ||
「扇形 中心 角 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 | ||
「扇形 中心 角 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 |  | |
「扇形 中心 角 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
「扇形 中心 角 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
「扇形 中心 角 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
「扇形 中心 角 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
「扇形 中心 角 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「扇形 中心 角 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「扇形 中心 角 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |
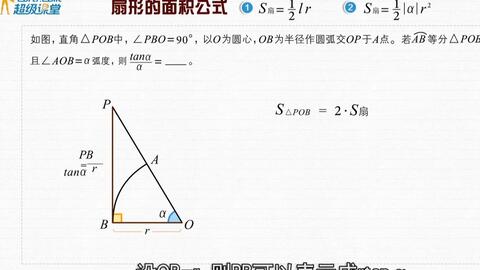
先ほど説明したように,半径1の扇形においては(中心角)=(弧の長さ)なので$\theta$でした. 左の扇形(半径1)と右の扇形(半径$r$)の相似比は$1r$ですから,弧の長さも当然$1r$となります. よって, 半径$r$の扇形の弧の長さは$r\theta$となりますね. 面積の公式扇形周长公式 因为扇形=两条半径+弧长 若半径为R,扇形所对的圆心角为n°,那么扇形周长: C=2R+nπR÷180 扇形面积公式 在半径为R的圆中,因为360°的圆心角所对的扇形的面积就是圆面积S=πR^2,所以圆心角





0 件のコメント:
コメントを投稿